第12題：外心問題, 設O為△ABC之外心，已知AB=6，BC=2√7，AC=4，且AO = r AB + s AC

第12題：外心問題, 設O為△ABC之外心，已知AB=6，BC=2√7，AC=4，且AO = r AB + s AC

題目重述

設 為 的 外心（circumcenter），已知

且

求：

(1) ______。

(2) ______。

---

答案（先給結論）

---

詳解（步驟 1 — 4，每步都配圖）

步驟 1：在坐標平面固定點位（方便計算）

為方便計算，選取座標使一邊為 x 軸。

取

（因為 ，把 放在 x 軸上，長度為 6）。

設 。由題給距離得

把兩式相減：

展開：

代回 ：

因此

對應圖（Step 1）：展示 A,B,C 座標與三角形。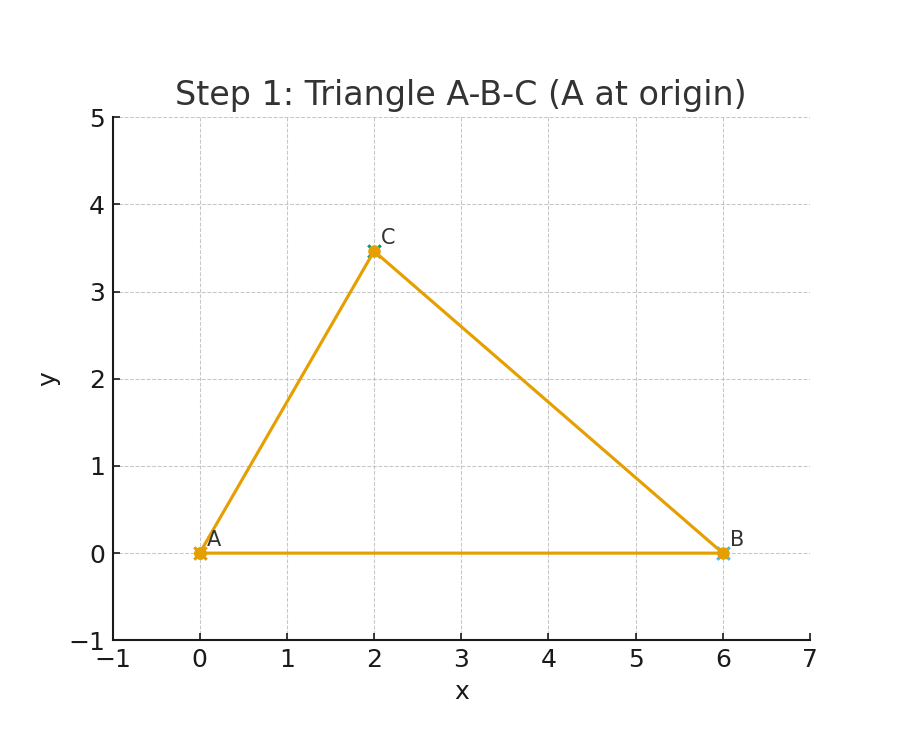

---

步驟 2：寫出向量 ，並計算內積

向量（以座標差表示）：

內積定義（坐標形式）：

所以

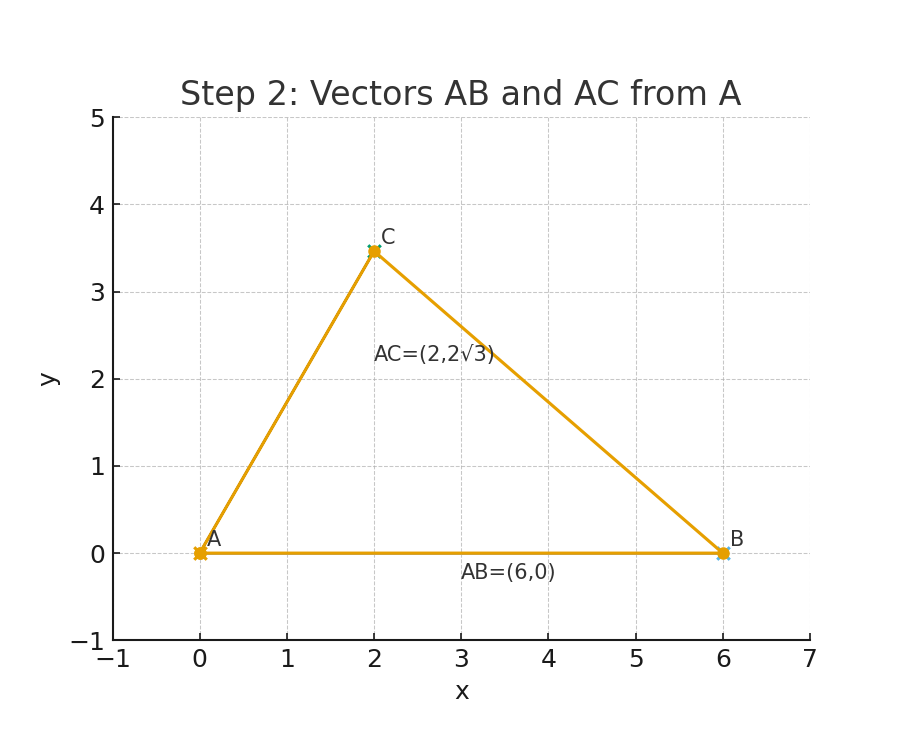
對應圖（Step 2）：從 A 出發畫出 與 ；在圖上註明分量。

步驟 3：求外心 （circumcenter）

幾何事實：外心為三角形三邊的垂直平分線交點。

1. 的中點為 。
   由於 在 x 軸，其垂直平分線是直線 。

2. 的中點：
   
   的斜率 ，因此 的垂直平分線斜率為 。
   方程式：
   
   將 代入：
   
   

因此

對應圖（Step 3）：垂直平分線與外心 O。

---

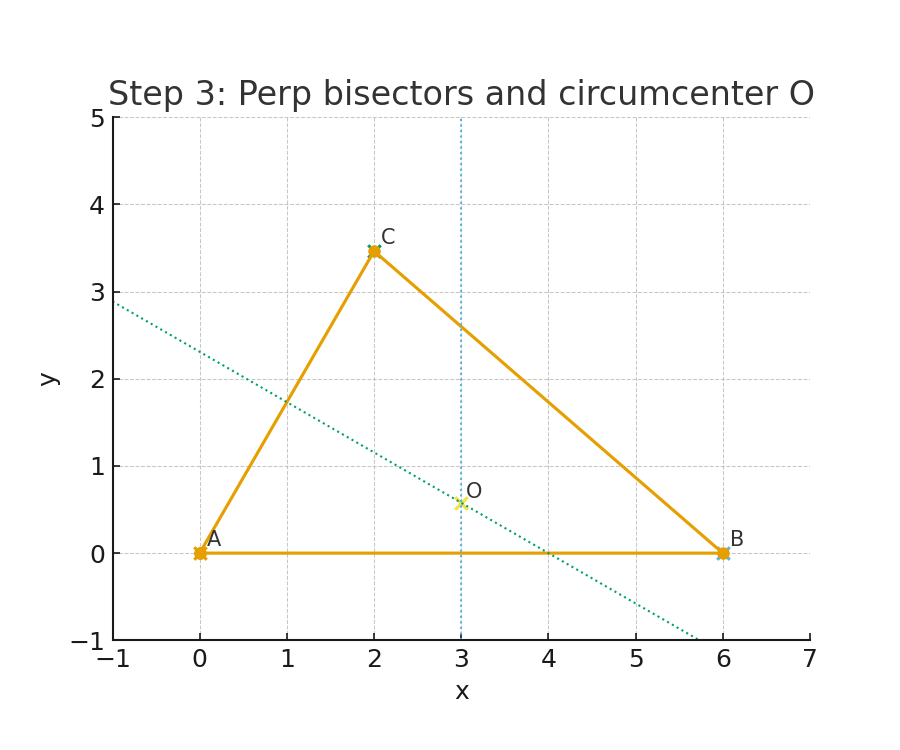
步驟 4：寫出 並以 展開求

已知 ，所以

假設

比較分量：

由第二式得

代入第一式：

因此

對應圖（Step 4）：畫出 ，並用箭頭示範 。

---

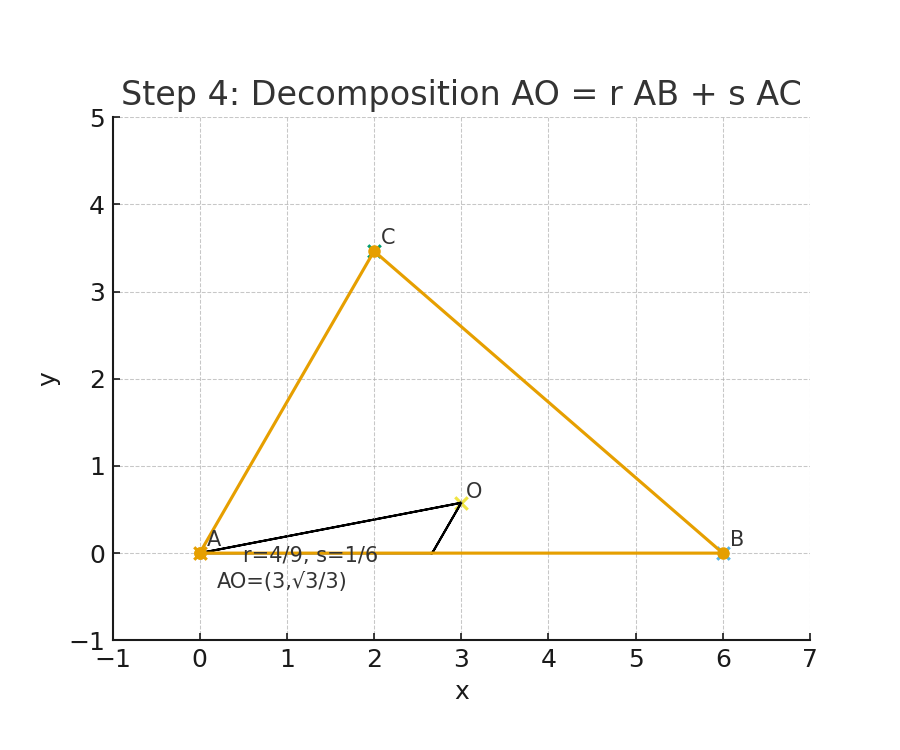
驗算

代回檢查：

與 相符 ✔

---

解題思考方向

1. 把題目轉成座標問題：放一邊在 x 軸，化簡計算。
2. 用分量法計算內積：最直接。
3. 外心是垂直平分線交點：這是關鍵幾何性質。
4. 向量分解：轉成聯立方程解 。
5. 驗算：代回確認正確性。