第13題：設H為△ABC之垂心，已知AB=4，BC=6，AC=5，且AH = x AB + y AC，試求數對 (x, y) = ?

第13題：設H為△ABC之垂心，已知AB=4，BC=6，AC=5，且AH = x AB + y AC，試求數對 (x, y) = ?

答案

也就是

---

解題方向（高中生斜率版）

已知：.

1. 設斜率與直線方程

   我們把 當作原點， 放在 x 軸上：

   設 ，由邊長：

   相減得：

   再求 ：

   所以

2. 求高的斜率

   直線斜率公式：

   • 邊 的斜率：

   • 邊 的斜率：

   高的斜率互為負倒數：

   • 點的高（垂直於 ）：

   • 點的高（垂直於 ）：

3. 求垂心 H

   高的方程式：

   令兩高交點：

   兩邊乘 ：

   再代回：

   所以

4. 向量表示 AH = x AB + y AC

   向量座標：

   解線性方程組：

   所以

---

情境式說法

想像你在操場上的 A 點，前面有兩個方向：

• 向右走到 B（那條方向叫 AB），全長 4 步；
• 斜斜往前走到 C（那條方向叫 AC），全長 5 步。

現在我們說「到 H 的路」可以拆成：

1. 先沿著 AB 走 的距離（也就是 步）；
2. 再沿著 AC 走 的距離（也就是 步）；

把這兩段走完，你就會到達 H。
所以 AH = AB + AC —— 就像把一段路拆成「向右走一小段＋斜斜走一小段」來到目標。

---

為什麼用到的定理／技巧（要點）

1. 斜率概念：直線斜率 = 高度 / 水平距離，兩直線垂直則斜率互為負倒數。
2. 正交心（Orthocenter）：三角形三條高互相交於一點 H。
3. 向量線性組合：可以把 AH 拆成 AB 和 AC 的組合（解 線性方程組）。

---

生活中的應用

把一個向量表示成兩個方向的組合，在物理工程、電腦繪圖、導航、力的分解時非常常見。例如：

• 把合力拆成「東向力」和「北東向力」的分量；
• 路徑規劃：先沿道路 A 的方向走一段，再沿道路 C 的方向走一段到目的地。

---

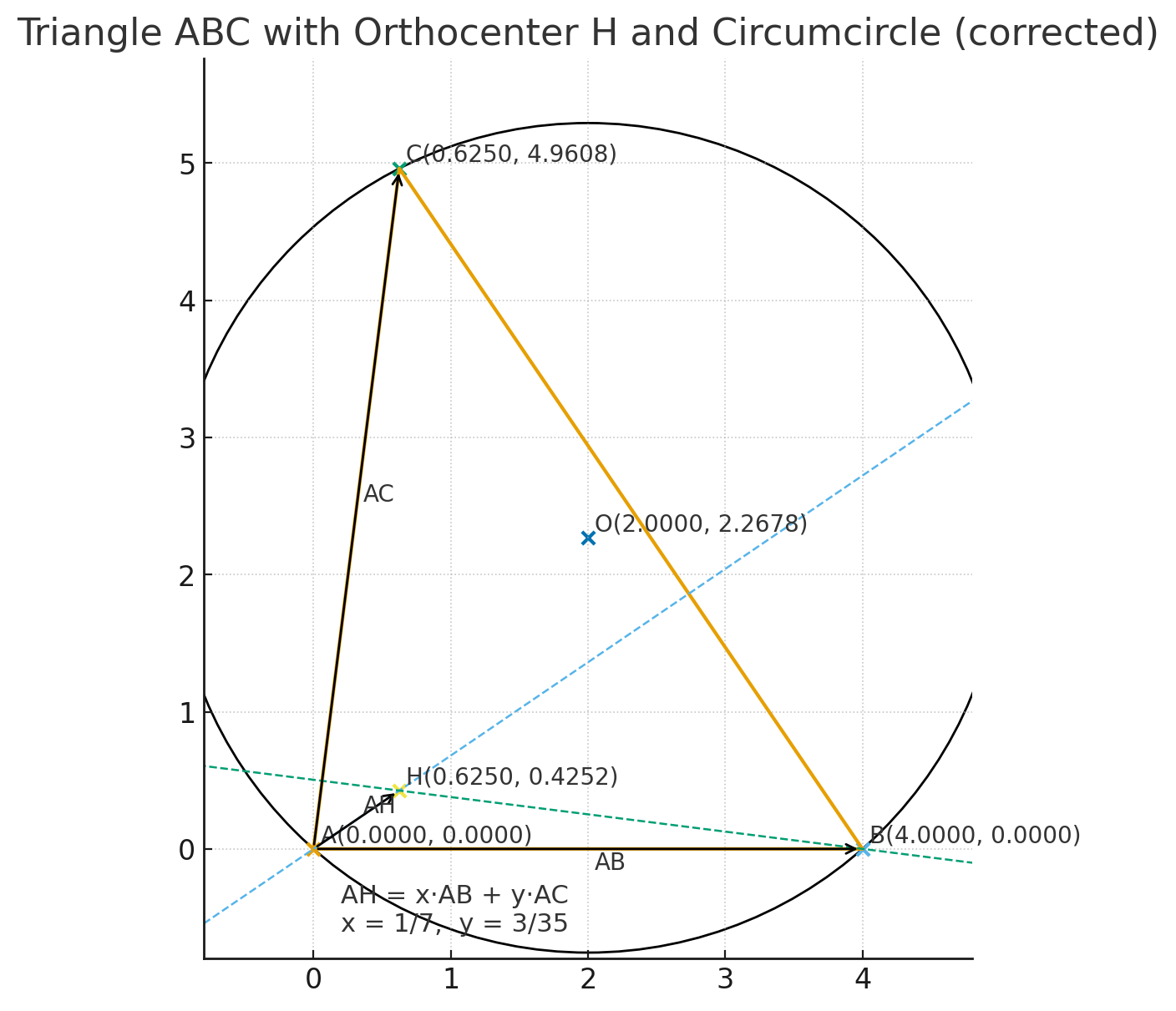
圖的說明