向量應用題詳解:利用線性組合與面積比求解 (x,y) 與子三角形面積
向量應用題詳解:利用線性組合與面積比求解 (x,y) 與子三角形面積
解答與詳解
題目:
設
(1) 數對
(2)
🥇 第一步:畫圖
三角形
畫好一張示意圖(先看位置就好):
📌 點 A 在左下角
📌 點 B 在右下角
📌 點 C 在左上角
📌 點 P 在三角形裡面(有點靠近中間)
📌 點 D 在邊
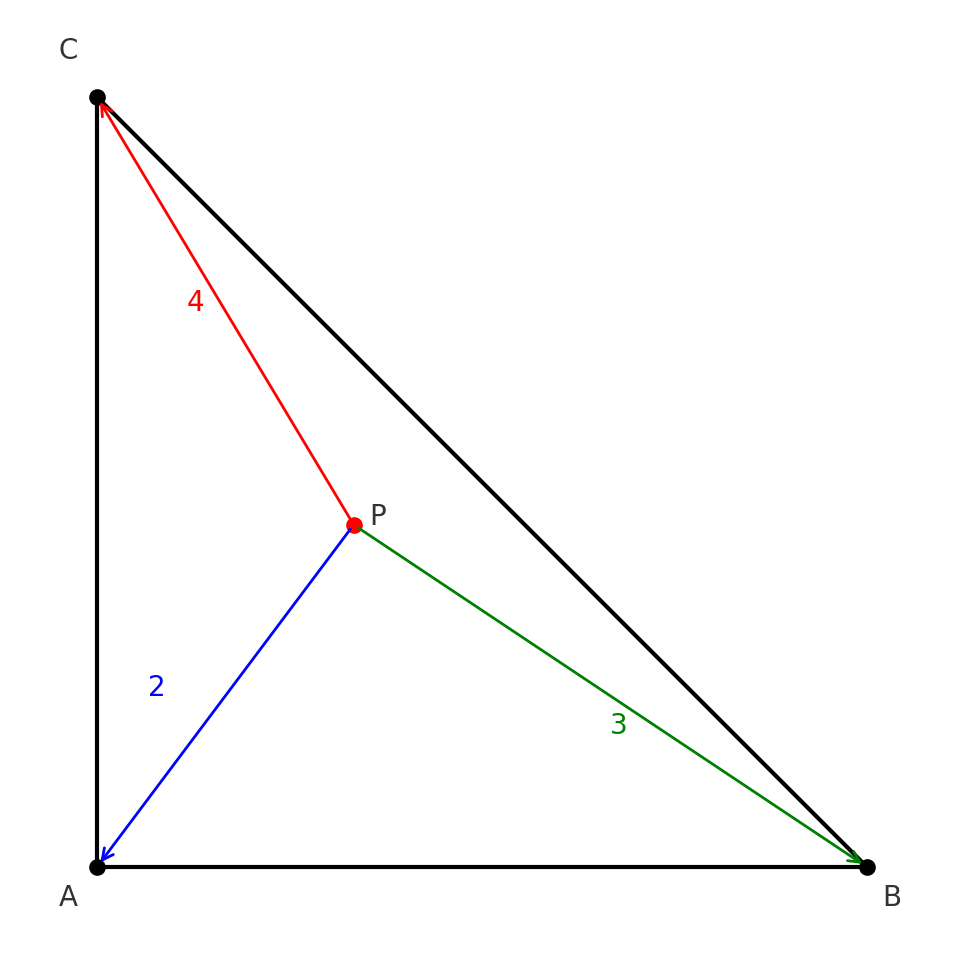
🥈 第二步:翻譯題目成故事
題目說:
我們把它想成 三個小朋友在拉一個橡皮筋:
- 小朋友 A 用「力量 2」把橡皮筋拉向
- 小朋友 B 用「力量 3」把橡皮筋拉向
- 小朋友 C 用「力量 4」把橡皮筋拉向
結果三個人的力量剛好平衡 → 橡皮筋(也就是
👉 所以
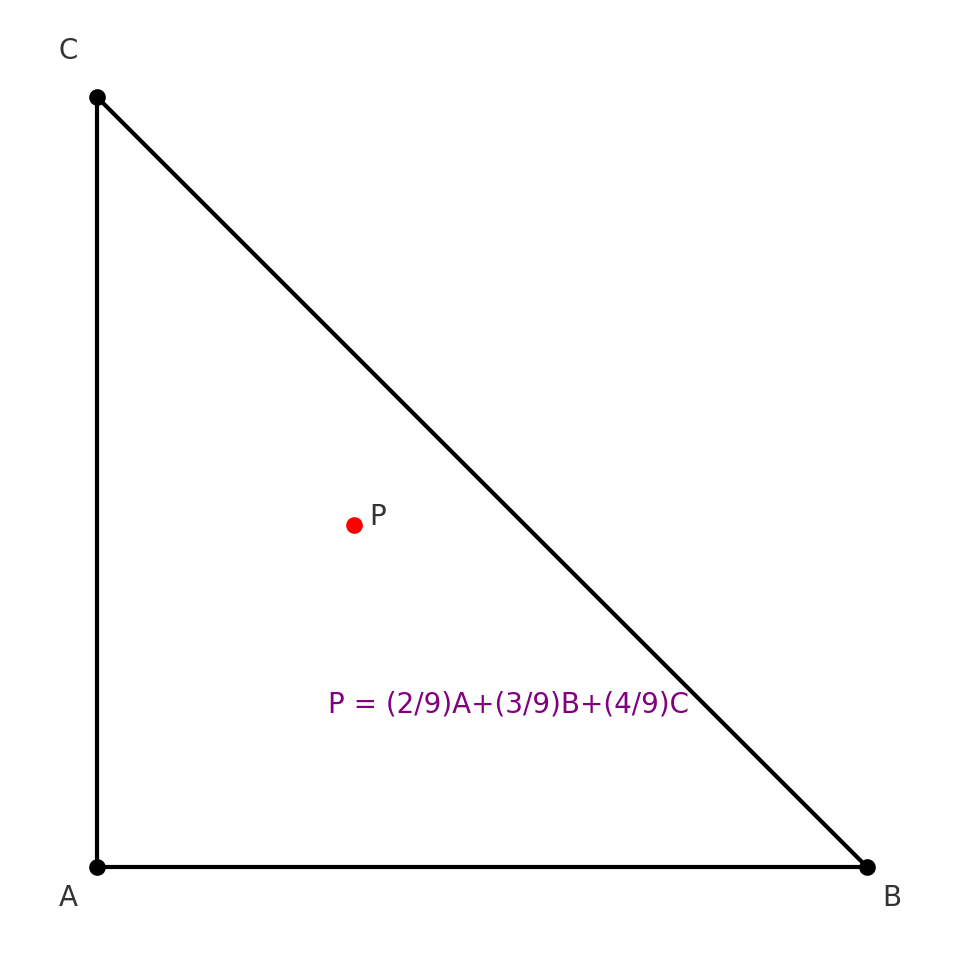
🥉 第三步:翻成數學
這種「比重」其實就是一種「加權平均」。
題目給的係數是
所以
👉 意思是:
這樣我們就知道:
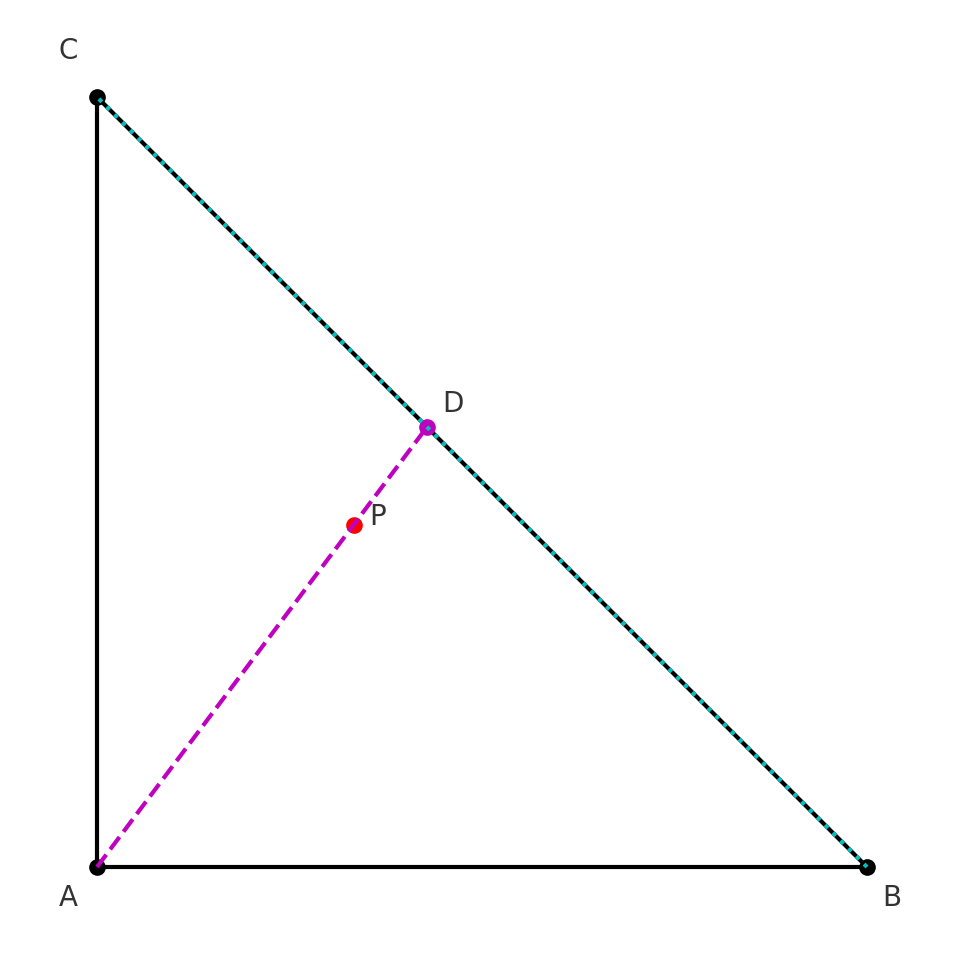
🥇 第四步:找到
因為
依照分點公式:
🥈 第五步:翻成「向量式」
題目要的是
我們已經知道
所以
👉 這裡就看出來:
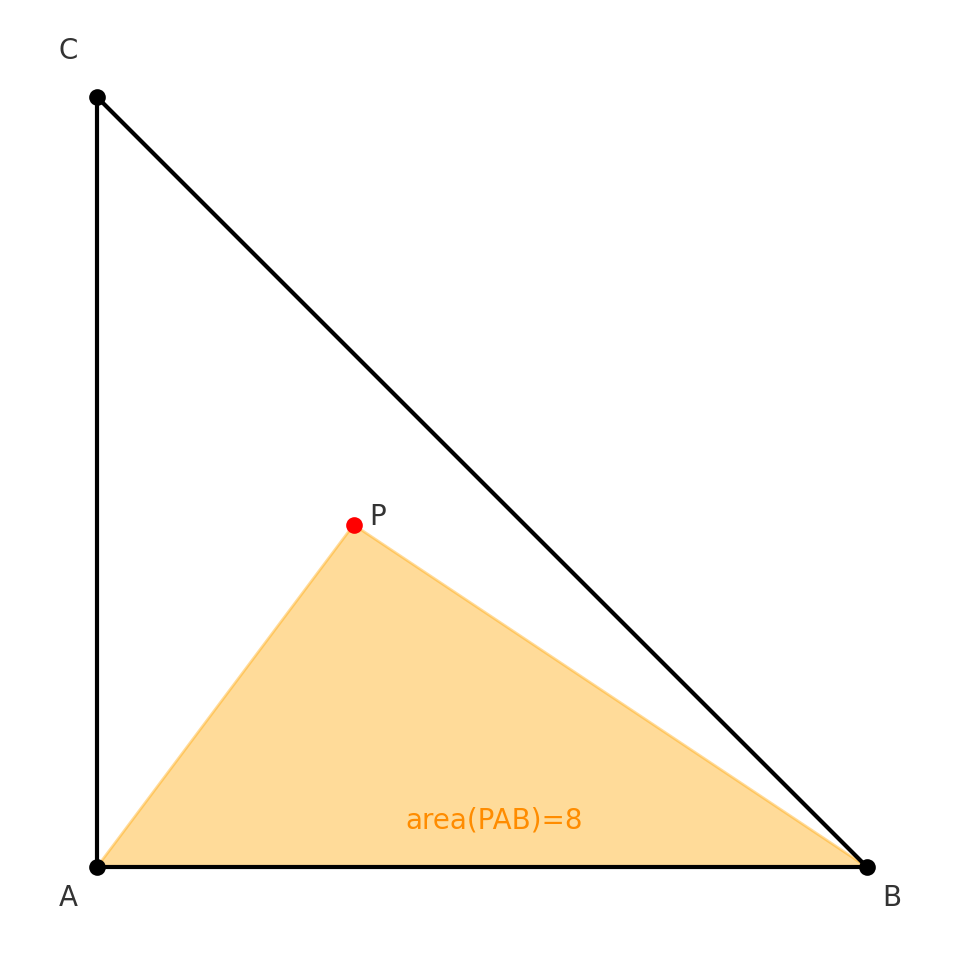
🥉 第六步:算面積
題目說
因為
👉 在面積上也有一個規則:
總和
所以 1 份 =
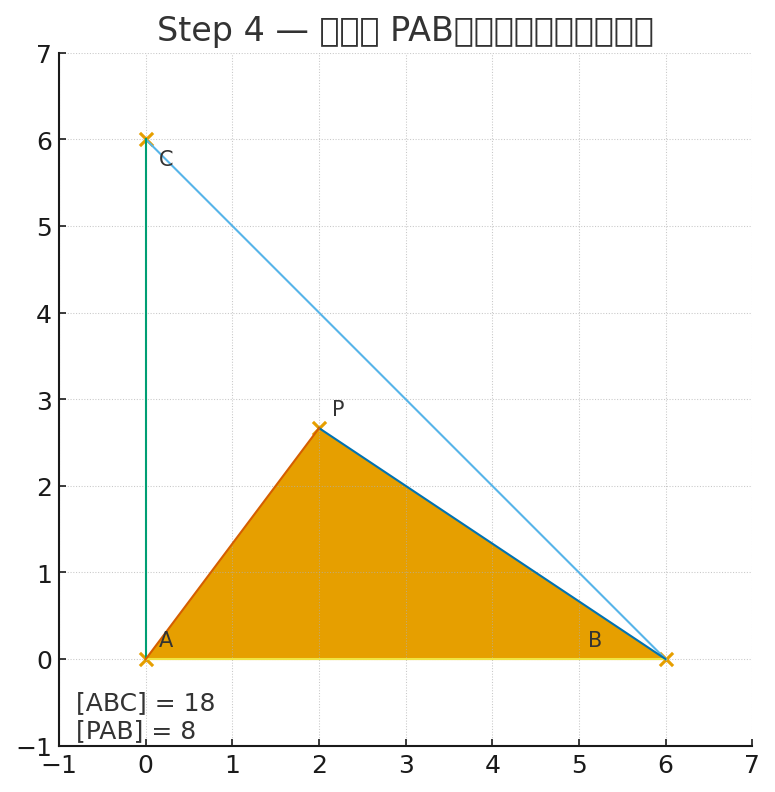
🎉 最後答案
(1)
(2)