Vector-005 在△ABC中,AD交BCD點,BE交AD於E點,且∠ACB = 30°,∠EDB = 60°,∠AEB =120°。若CD=15,ED=7,則AB=
Vector-005 在△ABC中,AD交BCD點,BE交AD於E點,且∠ACB = 30°,∠EDB = 60°,∠AEB =120°。若CD=15,ED=7,則AB=
結論：**
最後的綜合圖：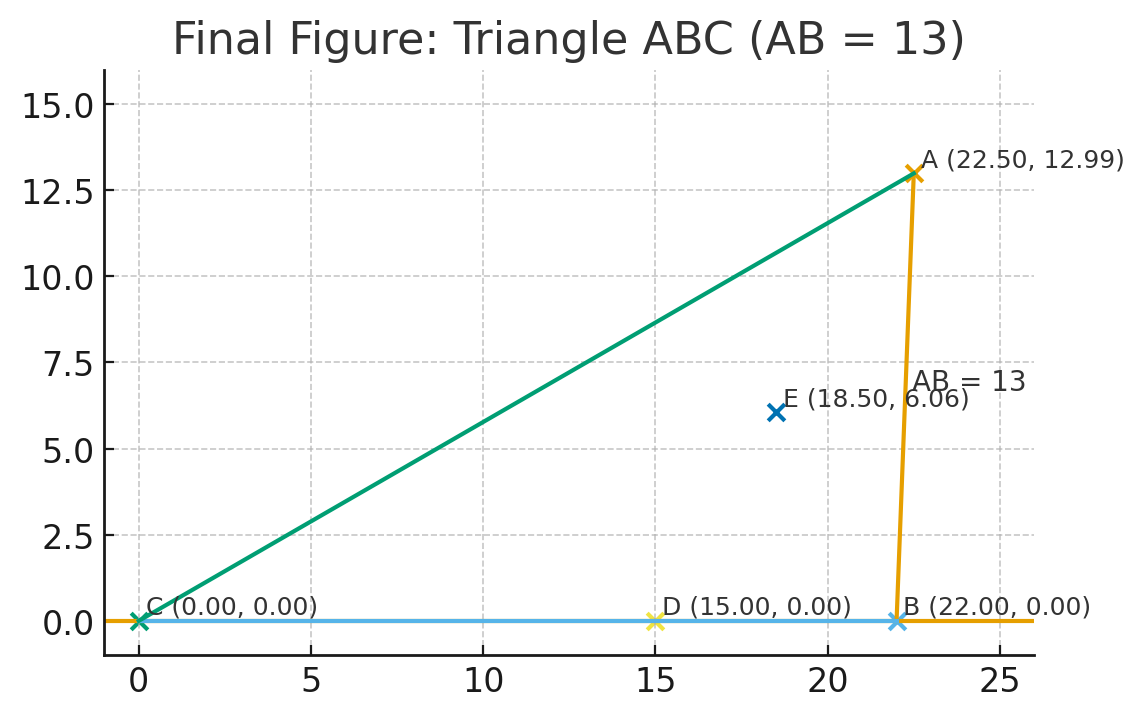
步驟 1：座標化 + 利用已知角度找 A（圖 1）
想法：把 C 放在原點，將 BC 放在 x 軸上，可以把角度轉成直線斜率或方程式，使幾何問題變成解代數方程，計算方便且系統化。
設
（因為題目給，且 D 在 BC 上） 由
，直線 CA 的斜率為
因此直線 CA 方程為由
且 E 在 AD 上，可得直線 AD 通過 D(15,0)，方向角為 60°： 將兩直線聯立求交點 A：
所以
（圖 1：顯示 C 為原點，從 C 作 30° 射線、從 D 作 60° 射線，交點為 A）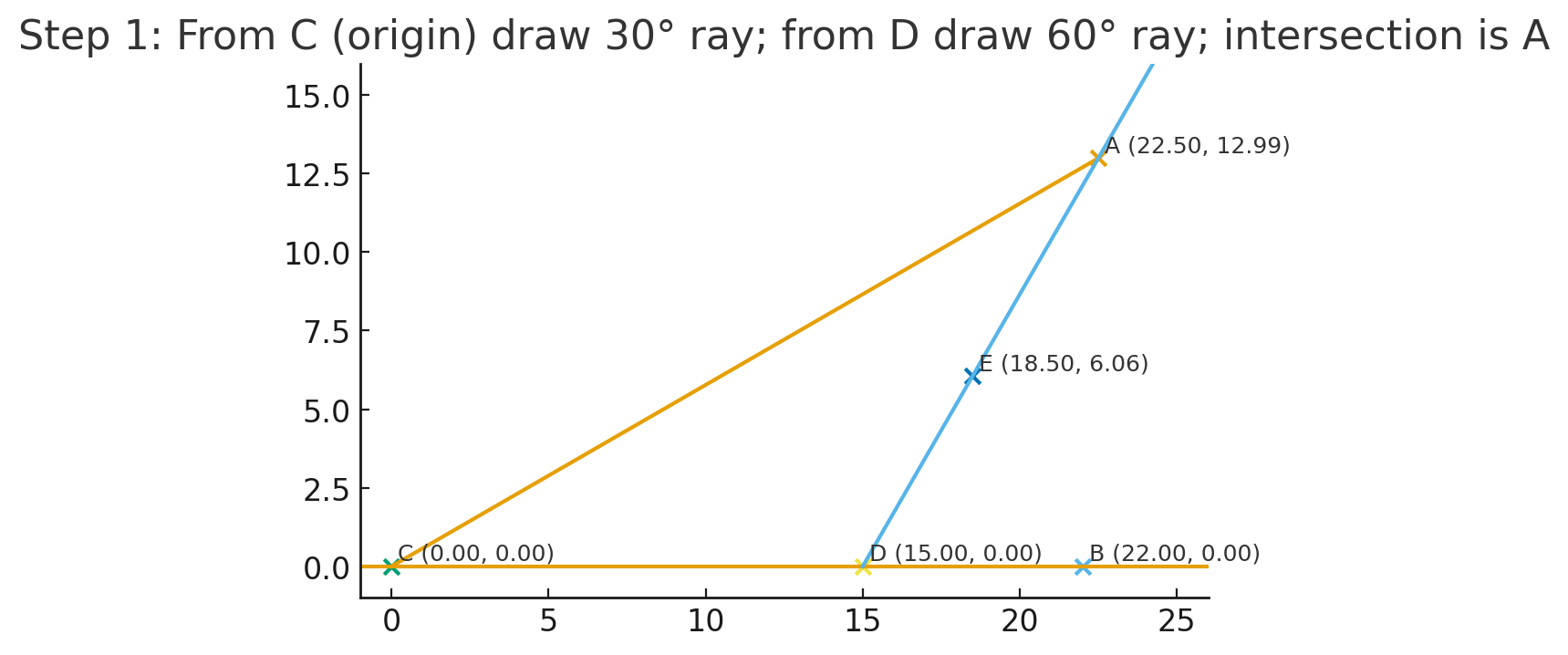
檢查 AC 長度：
步驟 2：利用 AD 的方向找 E（圖 2）
已知
AD 長度：
AE = AD - ED = 8
AD 單位向量：
從 D 往上量 7 得 E：
檢查：
（圖 2：標示 AD=15, ED=7, AE=8）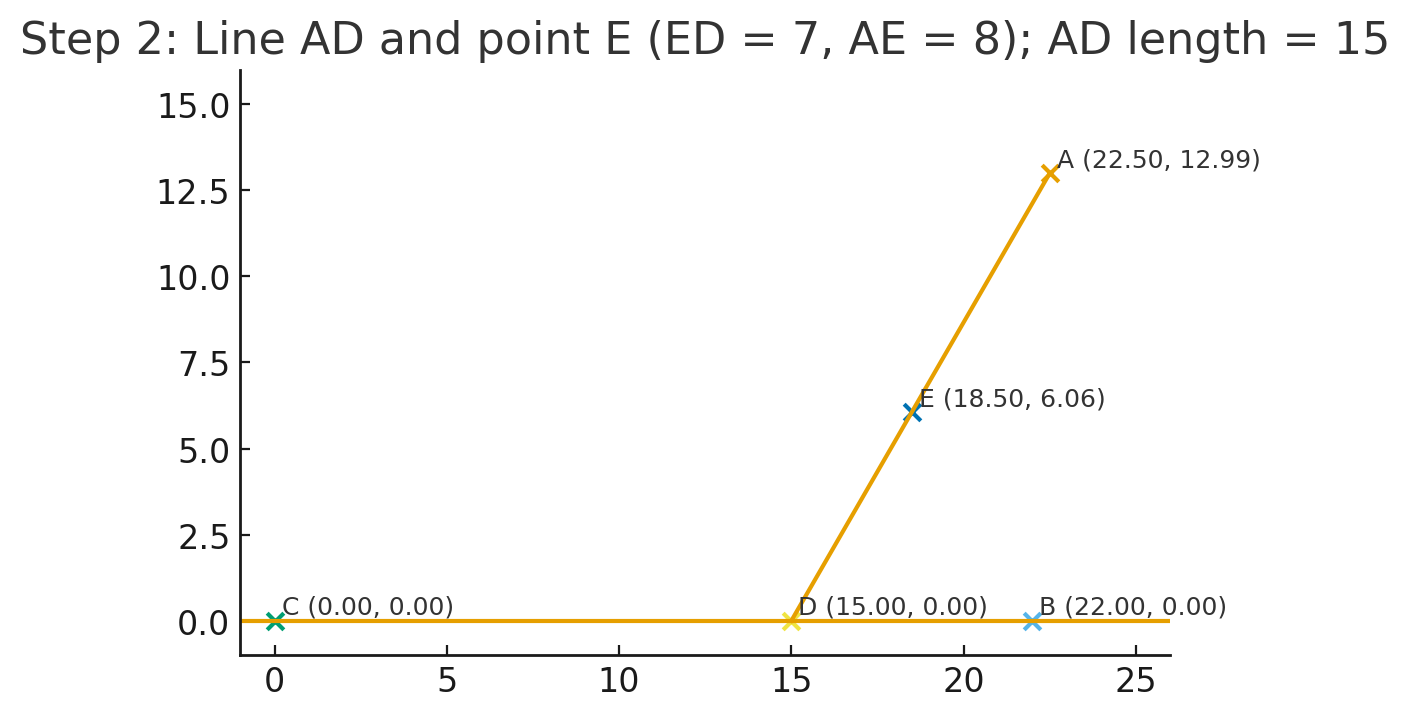
步驟 3：以
設 B=(b,0)，則
內積公式：
代數計算：
平方並整理：
所以
（圖 3：標示 B 與 E，角 AEB=120°）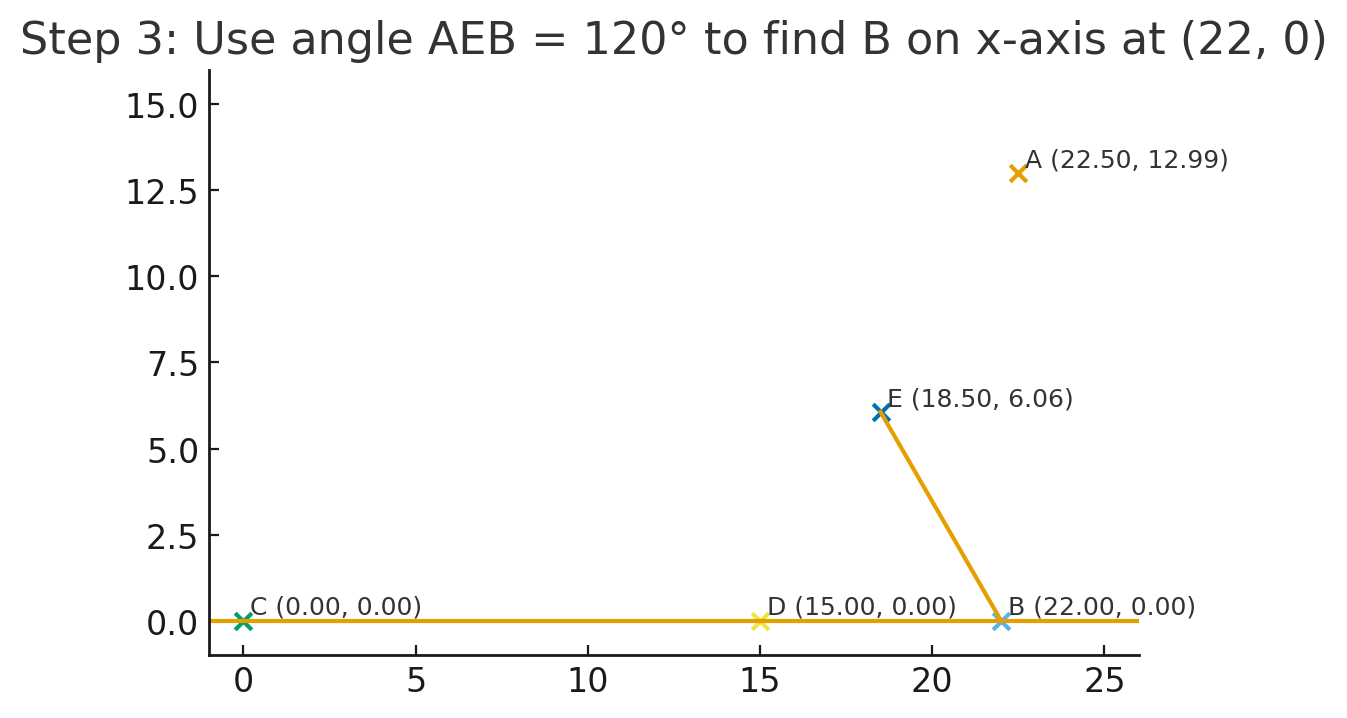
步驟 4：計算
（圖 4：完整三角形 ABC，標示 AB=13）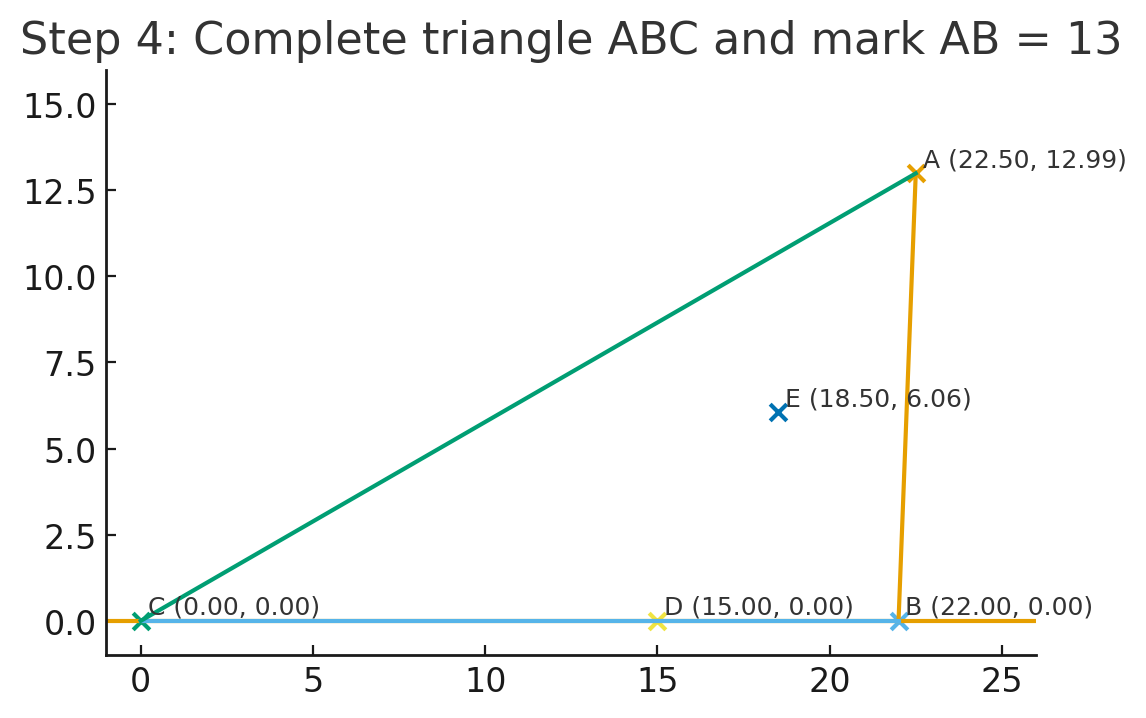
總結
最終答案：
解題思路回顧：
- 座標化：C 放原點，BC 放 x 軸，把角度轉成直線斜率。
- 用 AD 的方向與已知 ED 長度定位 E。
- 用
把角度轉成向量內積代數式，解出 B。 - 計算 AB 距離。
向量與三角函數簡單說明
向量：有大小與方向，兩點 P(x1,y1), Q(x2,y2) 的向量
內積：
三角函數：
記憶口訣：SOH CAH TOA常用角度：
角度 sin cos tan 30° 1/2 √3/2 1/√3 45° √2/2 √2/2 1 60° √3/2 1/2 √3 畢氏恒等式：
小練習
- 梯子長 10，角 30°，高度：
- 梯子底端前進距離：
- 斜率：